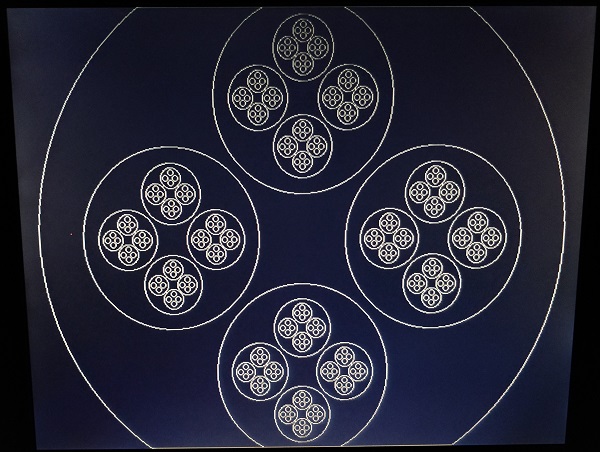
This program was my attempt to draw fractals on a VGA screen using Prof. Hunter Adam's VGA Library for the RaspberryPi Pico. The resources for the project include the C SDK User Guide, the RP2040 Datasheet and Prof. Hunter's website. I also used the Nature of Code series by Daniel Shiffman as a starting point for studying fractals.
According to Nature of Code's fractal page, the term fractal (from the Latin fractus, meaning “broken”) was coined by the mathematician Benoit Mandelbrot in 1975. In his seminal work “The Fractal Geometry of Nature,” he defines a fractal as “a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole.” In short, a fractal is a shape which when divided into various parts, each part can represent the figure as a whole.
The repeated application of a rule to successive results is known as recursion. One of the most famous applications for recursion is the calculation of factorical. The factorial of a natural number is defined as:
\begin{align} n! &= n \times (n-1)! \\ 0! &= 1 \end{align}For instance, solving for 5! looks like: \begin{align} 5! &= 5 \times 4! \\ 5! &= 5 \times 4 \times 3! \\ 5! &= 5 \times 4 \times 3 \times 2! \\ 5! &= 5 \times 4 \times 3 \times 2 \times 1! \\ 5! &= 5 \times 4 \times 3 \times 2 \times 1 \\ 5! &= 120 \end{align}
Note: Recursions must always have a base case and that too at a reasonable depth, else it will cause a stack overflow error.
/*
* Parth Sarthi Sharma (pss242@cornell.edu)
* Code based on examples from Raspberry Pi Foundation.
* This code is an implementation of a circle fractal
* on the Raspberry Pi Pico to draw a pattern. The pattern is developed
* by recursively calling a function by reducing a parameter until a base condition is met.
*/
#include <stdio.h> //The standard C library
#include <math.h> //The standard math library
#include "pico/stdlib.h" //Standard library for Pico
#include "hardware/pio.h" //The hardware PIO library
#include "hardware/dma.h" //The hardware DMA library
#include "pico/time.h" //The pico time library
#include "hardware/gpio.h" //The hardware GPIO library
#include "pico/multicore.h" //The pico multicore library
#include "vga_graphics.h" //The graphics library
#define HEIGHT 480 //Height of the VGA screen
#define WIDTH 640 //Width of the VGA screen
void makeCircleFractal(int x, int y, float radius){ //Function to recursively draw a circle fractal
drawCircle(x, y, radius, WHITE); //Draw a circle
if(radius > 8){ //If the radius is greater than 8
makeCircleFractal(x + radius / 2, y, radius / 3); //Start another function with shifted x-coordinate and 1/3rd the radius
makeCircleFractal(x - radius / 2, y, radius / 3); //Start another function with shifted x-coordinate and 1/3rd the radius
makeCircleFractal(x, y + radius / 2, radius / 3); //Start another function with shifted y-coordinate and 1/3rd the radius
makeCircleFractal(x, y - radius / 2, radius / 3); //Start another function with shifted y-coordinate and 1/3rd the radius
}
}
int main(){ //The program running on core 0
stdio_init_all(); //Initialize all of the present standard stdio types that are linked into the binary
initVGA(); //Initialize the VGA screen and functions
makeCircleFractal(WIDTH / 2, HEIGHT / 2, 300); //Start the fractal function from the centre of the screen with 300 radius
}

cmake_minimum_required(VERSION 3.13)
include(pico_sdk_import.cmake)
project(CircleFractal-project)
pico_sdk_init()
add_executable(CircleFractal)
pico_enable_stdio_usb(CircleFractal 1)
pico_enable_stdio_uart(CircleFractal 1)
pico_generate_pio_header(CircleFractal ${CMAKE_CURRENT_LIST_DIR}/hsync.pio)
pico_generate_pio_header(CircleFractal ${CMAKE_CURRENT_LIST_DIR}/vsync.pio)
pico_generate_pio_header(CircleFractal ${CMAKE_CURRENT_LIST_DIR}/rgb.pio)
target_sources(CircleFractal PRIVATE CircleFractal.c vga_graphics.c)
target_link_libraries(CircleFractal PRIVATE pico_stdlib hardware_pio hardware_dma hardware_adc hardware_irq pico_time pico_multicore)
pico_add_extra_outputs(CircleFractal)